Leveraging the advanced tools developed in the field of network science to facilite the understanding of complex configurable systems in different domains.

Our Work #

Publications #

1. Exploring Structural Similarity in Fitness Landscapes via Graph Data Mining: A Case Study on Number Partitioning Problems
   Mingyu Huang and Ke Li
   Proc. of the 32nd International Joint Conference on Artificial Intelligence (IJCAI'23)
   2023 | Conference Paper | Abs | PDF | Supp | BiB |

   One of the most common problem-solving heuristics is by analogy. For a given problem, a solver can be viewed as a strategic walk on its fitness landscape. Thus if a solver works for one problem instance, we expect it will also be effective for other instances whose fitness landscapes essentially share structural similarities with each other. However, due to the black-box nature of combinatorial optimization, it is far from trivial to infer such similarity in real-world scenarios. To bridge this gap, by using local optima network as a proxy of fitness landscapes, this paper proposed to leverage graph data mining techniques to conduct qualitative and quantitative analyses to explore the latent topological structural information embedded in those landscapes. In our experiments, we use the number partitioning problem as the case and our empirical results are inspiring to support the overall assumption of the existence of structural similarity between landscapes within neighboring dimensions. Besides, experiments on simulated annealing demonstrate that the performance of a meta-heuristic solver is similar on structurally similar landscapes.
   

Analysis Methods #

Statistical Features #

Landscape Visualization #

High-Level Topological Features #

Case Studies #

Classic BBOPs #

AutoML #

HousePrice-Train

HousePrice-Test

Stone-Train

Stone-Test

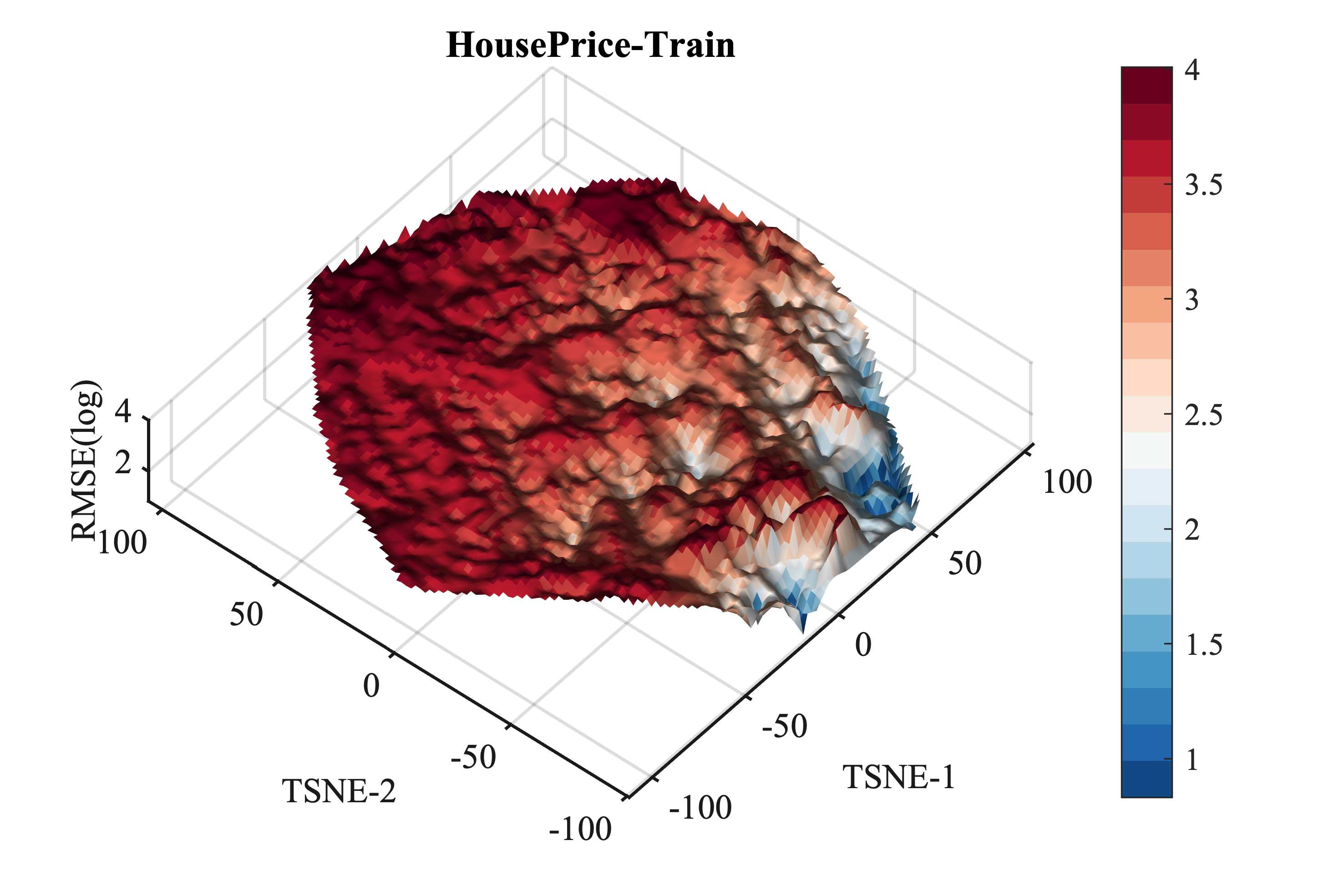
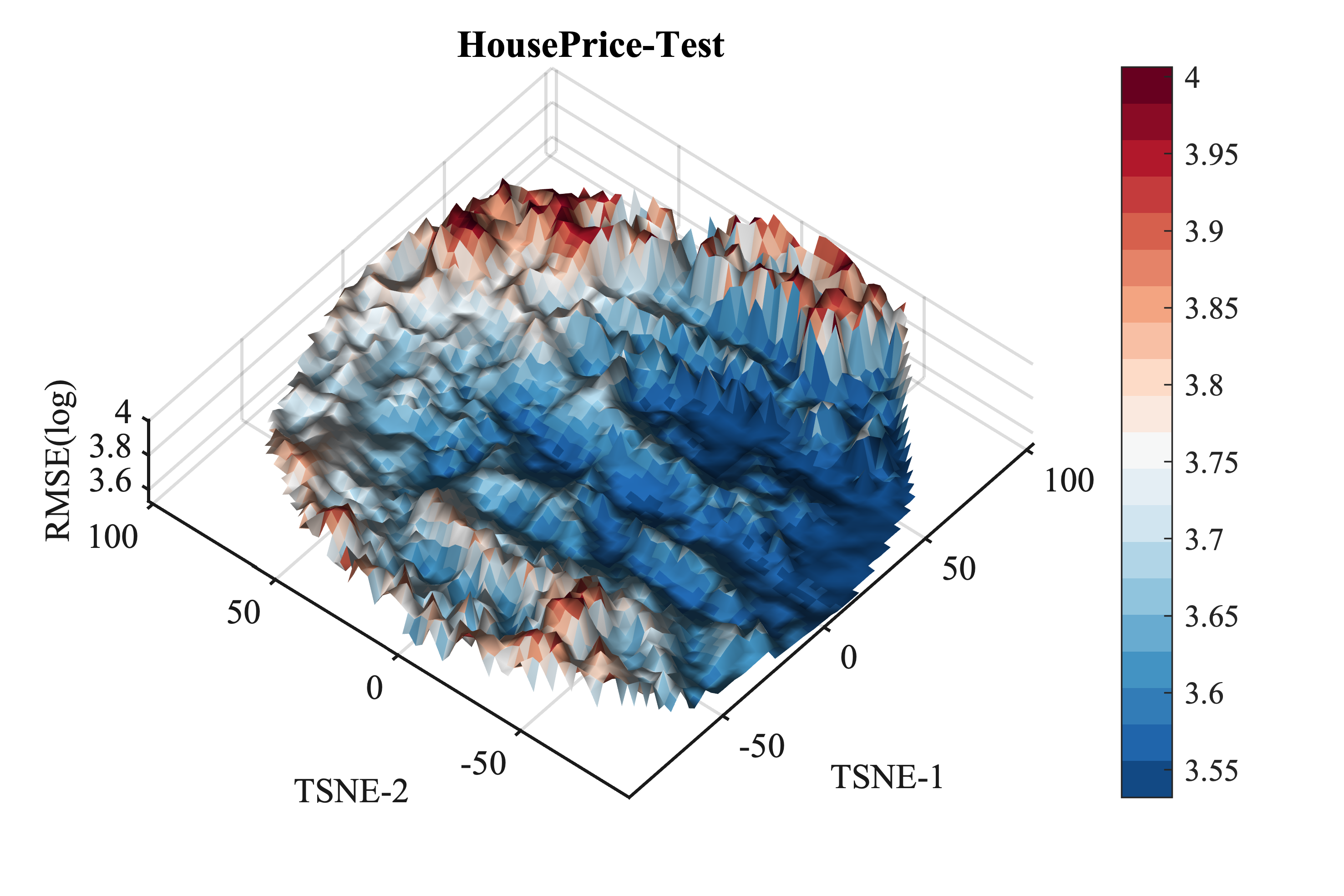
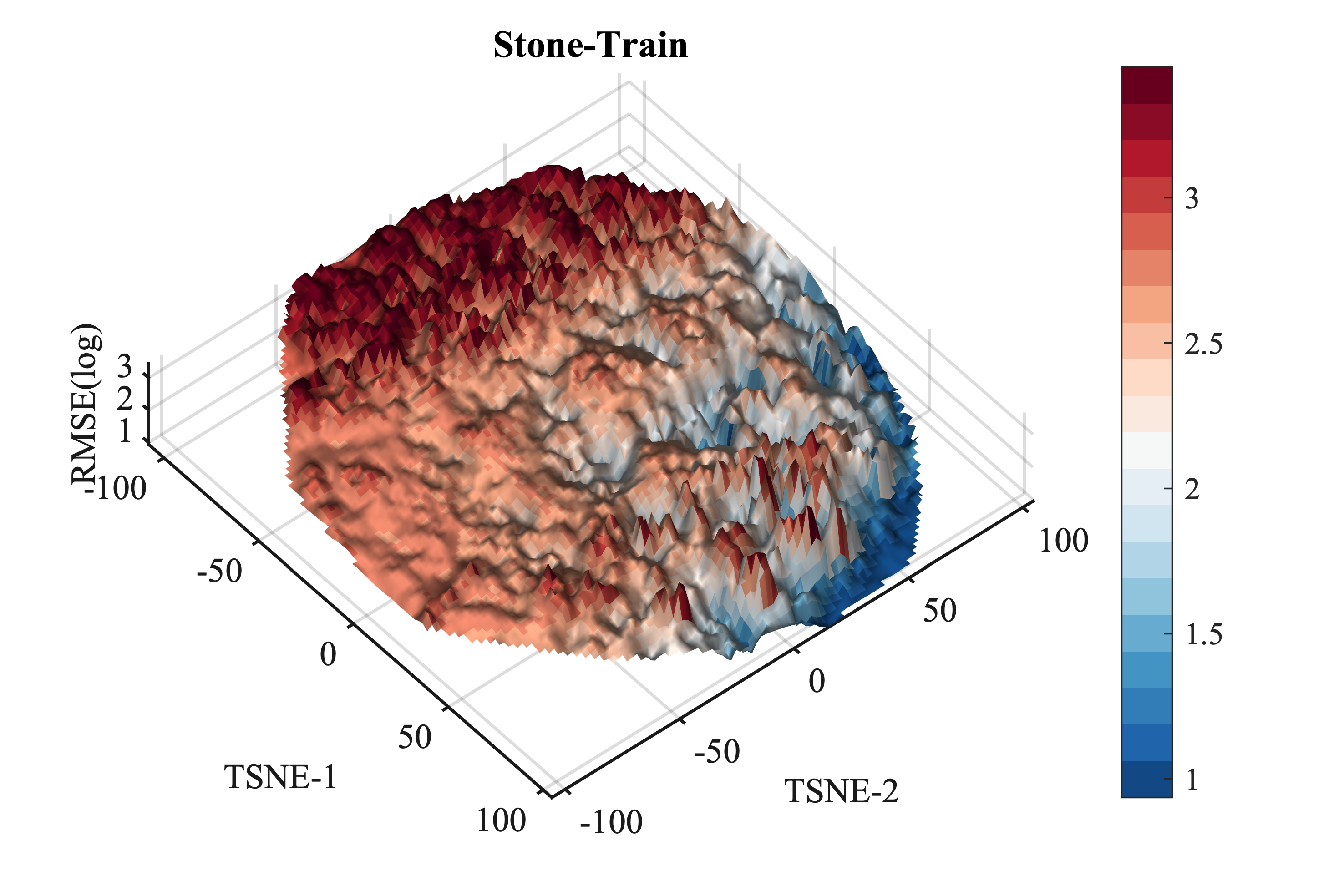
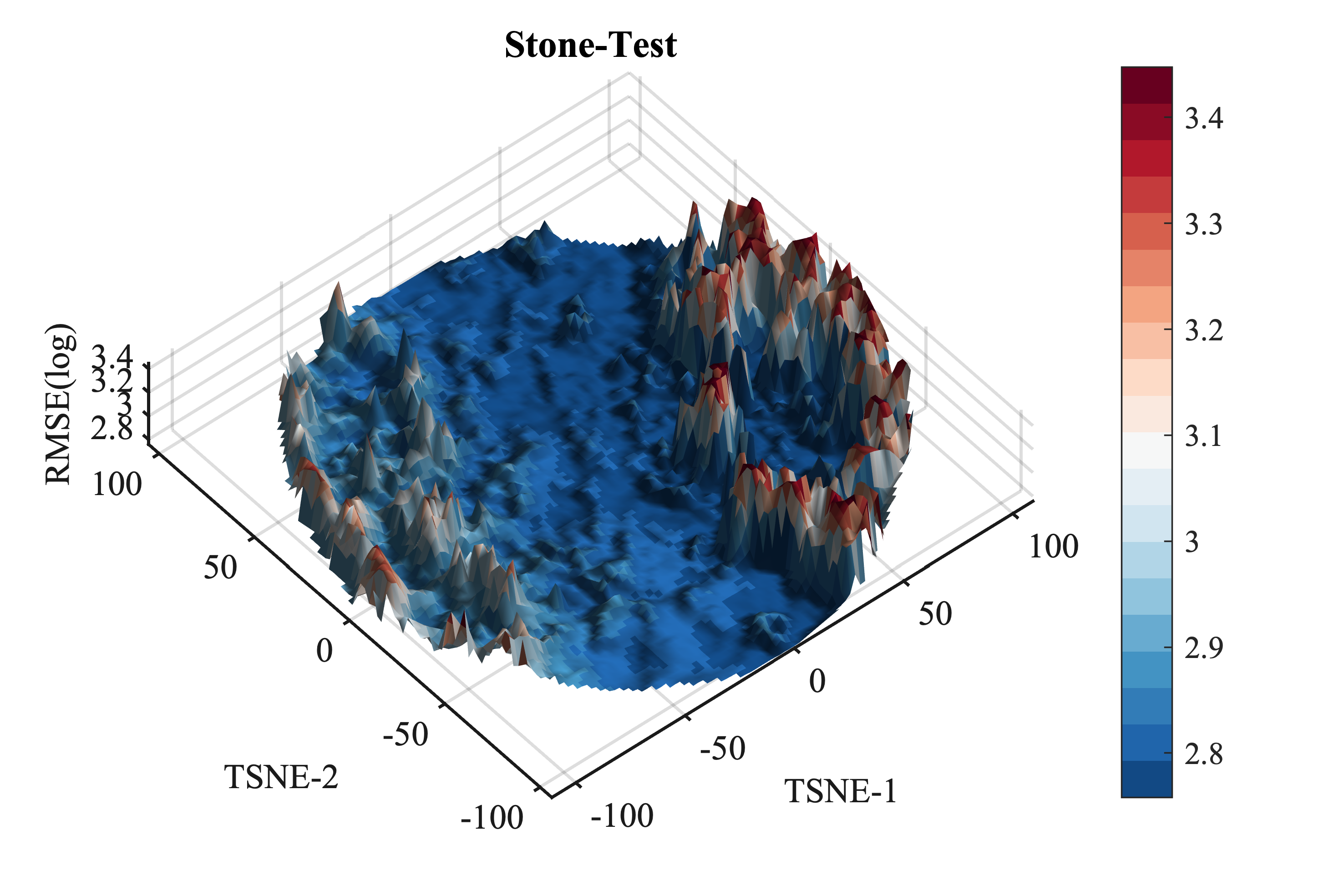
Software Engineering #

Resources #

• Paper List of Landscape Analysis

  1. Survey Papers
  2. Exploratory Landscape Analysis (ELA)
  3. Benchmarks
  4. Algorithm Selection Problem
  5. Instance Space Analysis
  6. Fitness Landscape Analysis (FLA)
  7. Problem-Specific
  8. Landscape Visualization

• Paper List of AutoML

• Projects and Websites

Paper List of Landscape Analysis #

Survey Papers

1. A Comprehensive Survey on Fitness Landscape Analysis
   Erik Pitzer and Michael Affenzeller
   Recent Advances in Intelligent Engineering Systems
   2012 | Survey Paper

2. A Survey of Techniques for Characterising Fitness Landscapes and Some Possible Ways Forward
   Katherine M. Malan and Andries Engelbrecht
   Information Sciences
   2013 | Survey Paper

3. A Survey of Advances in Landscape Analysis for Optimisation
   Katherine M. Malan
   Algorithms
   2021 | Survey Paper

4. A Survey of Landscape Analysis for Optimisation
   Feng Zou, Debao Chen, Hui Liu, Siyu Cao, Xuying Ji and Yan Zhang
   Neurocomputing
   2022 | Survey Paper

Exploratory Landscape Analysis (ELA)

1. Exploratory Landscape Analysis
   Olaf Mersmann, Bernd Bischl, Heike Trautmann, Mike Preuss, Claus Weihs and Gnter Rudolph
   Proc. of the 13th Annual Genetic and Evolutionary Computation Conference (GECCO'11)
   2011 | Conference Paper

2. Comprehensive Feature-Based Landscape Analysis of Continuous and Constrained Optimization Problems Using the R-Package Flacco
   Pascal Kerschke and Heike Trautmann
   Applications in Statistical Computing: From Music Data Analysis to Industrial Quality Improvement
   2019 | Book Chapter

3. Flaccogui: Exploratory Landscape Analysis for Everyone
   Christian Hanster, Pascal Kerschke
   Proc. of the 13th Annual Genetic and Evolutionary Computation Conference (GECCO'17)
   2017 | Conference Paper

4. Exploratory Landscape Analysis is Strongly Sensitive to the Sampling Strategy
   Quentin Renau, Carola Doerr, Johann Dreo and Benjamin Doerr
   Proc. of the International Conference on Parallel Problem Solving from Nature (PPSN’XVI)
   2020 | Conference Paper

5. Automated Algorithm Selection on Continuous Black-Box Problems by Combining Exploratory Landscape Analysis and Machine Learning
   Pascal Kerschke and Heike Trautmann
   Evolutionary Computation
   2019 | Journal Paper

6. Benchmarking Evolutionary Algorithms: Towards Exploratory Landscape Analysis
   Olaf Mersmann, Mike Preuss and Heike Trautmann
   Proc. of the International Conference on Parallel Problem Solving from Nature (PPSN’XI)
   2010 | Conference Paper

Benchmarks

1. Real-Parameter Black-Box Optimization Benchmarking 2009: Noiseless Functions Definitions
   Nikolaus Hansen, Steffen Finck, Raymond Ros and Anne Auger
   INRIA
   2009 | Research Report

2. COCO: a platform for comparing continuous optimizers in a black-box setting
   Nikolaus Hansen, Anne Auger, Raymond Ros, Olaf Mersmann, Tea Tušar and Dimo Brockhoff
   Optimization Methods and Software
   2021 | Journal Paper

Algorithm Selection

1. Automated Algorithm Selection: Survey and Perspectives
   Pascal Kerschke, Holger H. Hoos, Frank Neumann and Heike Trautmann
   Evolutionary Computation
   2019 | Survey Paper

2. Algorithm selection for black-box continuous optimization problems: A survey on methods and challenges
   Mario A. Muñoz, Yuan Sun, Michael Kirley and Saman K. Halgamuge
   Information Science
   2015 | Survey Paper

3. Cross-disciplinary perspectives on meta-learning for algorithm selection
   Kate A. Smith-Miles
   ACM Computing Survey
   2009 | Survey Paper

4. Algorithm Selection for Combinatorial Search Problems: A Survey
   Lars Kotthoff
   Data Mining and Constraint Programming
   2016 | Book Chapter

5. SATzilla: Portfolio-based Algorithm Selection for SAT
   Lin Xu, Frank Hutter, Holger H. Hoos and Kevin Leyton-Brown
   Journal of Artificial Intelligence Research
   2008 | Journal Paper

6. Automated Algorithm Selection on Continuous Black-Box Problems by Combining Exploratory Landscape Analysis and Machine Learning
   Pascal Kerschke and Heike Trautmann
   Evolutionary Computation
   2019 | Journal Paper

7. Algorithm selection based on exploratory landscape analysis and cost-sensitive learning
   Bernd Bischl, Olaf Mersmann, Heike Trautmann and Mike Preuß
   Proc. of the 13th Annual Genetic and Evolutionary Computation Conference (GECCO'17)
   2017 | Conference Paper

8. Sequential Model-Based Optimization for General Algorithm Configuration
   Frank Hutter, Holger H. Hoos and Kevin Leyton-Brown
   Proc. of the 5th International Conference on Learning and Intelligent Optimization (LION'11)
   2011 | Conference Paper

9. ParamILS: An Automatic Algorithm Configuration Framework
   Frank Hutter, Holger H. Hoos, Kevin Leyton-Brown and Thomas Stützle
   Journal of Artificial Intelligence Research
   2009 | Journal Paper

10. ASlib: A benchmark library for algorithm selection
    Bernd Bischl, Pascal Kerschke, Lars Kotthoff, Marius Lindauer, Yuri Malitsky, Alexandre Fréchette, Holger Hoos, Frank Hutter, Kevin Leyton-Brown, Kevin Tierney and Joaquin Vanschoren
    Artificial Intelligence
    2016 | Journal Paper

Instance Space Analysis

1. Towards objective measures of algorithm performance across instance space
   Kate Smith-Miles, Davaatseren Baatar, Brendan Wreford and Rhyd Lewis
   Computers & Operations Research
   2014 | Journal Paper

2. Measuring Algorithm Footprints in Instance Space
   Kate Smith-Miles and Thomas T. Tan
   Proc. of the 2012 IEEE Congress on Evolutionary Computation (CEC'12)
   2012 | Conference Paper

Fitness Landscape Analysis (FLA)

Fitness Landscapes

1. Combinatorial Landscapes
   Christian M. Reidys and Peter F. Stadler
   SIAM Review
   2002 | Journal Paper

2. Fitness landscapes
   Peter F. Stadler
   Biological Evolution and Statistical Physics
   2002 | Book Chapter

Evolvability / Searchability

1. Fitness landscapes and evolvability
   Tom Smith, Phil Husbands, Paul Layzell and Michael O’Shea
   Evolutionary Computation
   2002 | Journal Paper | Fitness Evolvability

2. A Comprehensive View of Fitness Landscapes with Neutrality and Fitness Clouds
   Leonardo Vanneschi, Marco Tomassini, Philippe Collard, Sébastien Vérel, Yuri Pirola and Giancarlo Mauri
   Proc. of the European Conference on Genetic Programming (EuroGP'07)
   2007 | Conference Paper | Fitness Clouds, Neutrality

3. Where are bottlenecks in NK fitness landscapes?
   Sebastien Verel, Philippe Collard and Manuel Clergue
   Proc. of the 2012 IEEE Congress on Evolutionary Computation (CEC'03)
   2003 | Conference Paper | Fitness Clouds

4. Fitness Clouds and Problem Hardness in Genetic Programming
   Leonardo Vanneschi, Manuel Clergue, Philippe Collard, Marco Tomassini and Sébastien Vérel
   Proc. of the 2004 Annual Genetic and Evolutionary Computation Conference (GECCO'04)
   2004 | Conference Paper | Fitness Clouds

5. Fitness-Probability Cloud and a Measure of Problem Hardness for Evolutionary Algorithms
   Guanzhou Lu, Jinlong Li and Xin Yao
   Proc. of the European Conference on Genetic Programming (EuroGP'11)
   2011 | Conference Paper | Fitness Probability Clouds

Variable Interdependency / Epistasis

1. Epistasis Variance: A Viewpoint on GA-Hardness
   Yuval Davidor
   Foundations of Genetic Algorithms
   1991 | Journal Paper | Epistasis Variance

2. A Bit-Wise Epistasis Measure for Binary Search Spaces
   Cyril Fonlupt, Denis Robilliard and Philippe Preux
   Proc. of the International Conference on Parallel Problem Solving from Nature (PPSN’V)
   1998 | Conference Paper | Bit-wise Epistasis

3. The Effect of Spin-Flip Symmetry on the Performance of the Simple GA
   Bart Naudts and Jan Naudts
   Proc. of the International Conference on Parallel Problem Solving from Nature (PPSN’V)
   1998 | Conference Paper | Bit-wise Epistasis

4. Quantifying Variable Interactions in Continuous Optimization Problems
   Yuan Sun, Michael Kirley and Saman K. Halgamuge
   IEEE Transactions on Evolutionary Computation (TEVC)
   2017 | Journal Paper

Information / Deception

1. Sufficient Conditions for Deceptive and Easy Binary Functions
   Kalyanmoy Deb and David E. Goldberg
   Annals of Mathematics and Artificial Intelligence
   1994 | Journal Paper | Deception

2. Simple Genetic Algorithm and minimal deceptive problem,” University of Albana
   David. E. Goldberg
   Genetic Algorithms and Simulated Annealing
   1994 | Book Chapter | Deception

3. Genetic Algorithms and Walsh Functions: Part II, Deception and Its Analysis
   David E. Goldberg
   Complex Systems
   1989 | Journal Paper | Deception

4. Problem difficulty analysis for particle swarm optimization: deception and modality
   Bin Xin, Jie Chen and Feng Pan
   Proc. of the first ACM/SIGEVO Summit on Genetic and Evolutionary Computation (GEC'09)
   2009 | Conference Paper | Deception

Fitness Distance Correlation

1. Fitness Distance Correlation as a Measure of Problem Difficulty for Genetic Algorithms
   Terry Jones and Stephanie Forrest
   Proc. of the 6th International Conference on Genetic Algorithms (ICGA'95)
   1995 | Conference Paper | Fitness Distance Correlation

2. Fitness Distance Correlation Analysis: An Instructive Counterexample
   Lee Altenberg
   Proc. of the 7th International Conference on Genetic Algorithms (ICGA'97)
   1997 | Conference Paper | Fitness Distance Correlation

3. A Study of Fitness Distance Correlation as a Difficulty Measure in Genetic Programming
   Marco Tomassini, Leonardo Vanneschi, Philippe Collard and Manuel Clergue
   Evolutionary Computation
   2005 | Journal Paper | Fitness Distance Correlation

Local Optima, Basins of Attractions and Funnels

1. An Evaluation of Methods for Estimating the Number of Local Optima in Combinatorial Optimization Problems
   Leticia Hernando, Alexander Mendiburu and Jose A. Lozano
   Evolutionary Computation
   2013 | Journal Paper | Local Optima

2. Simple Random Sampling Estimation of the Number of Local Optima
   Khulood Alyahya and Jonathan E. Rowe
   Proc. of the International Conference on Parallel Problem Solving from Nature (PPSN’XIV)
   2016 | Conference Paper | Local Optima

3. Local Optima and Weight Distribution in the Number Partitioning Problem
   Khulood Alyahya and Jonathan E. Rowe
   Proc. of the International Conference on Parallel Problem Solving from Nature (PPSN’XIII)
   2014 | Conference Paper | Local Optima

4. PSO and multi-funnel landscapes: how cooperation might limit exploration
   Andrew M. Sutton, Darrell Whitley, Monte Lunacek and Adele Howe
   Proc. of the Annual Genetic and Evolutionary Computation Conference (GECCO'06)
   2006 | Conference Paper | Funnel

5. The dispersion metric and the CMA evolution strategy
   Monte Lunacek and Darrell Whitley
   Proc. of the Annual Genetic and Evolutionary Computation Conference (GECCO'06)
   2006 | Conference Paper | Funnel

6. A Closer Look Down the Basins of Attraction
   Erik Pitzer, Michael Affenzeller and Andreas Beham
   Proc. of the 2010 UK Workshop on Computational Intelligence (UKCI'10)
   2010 | Conference Paper | Basin of Attraction

7. Anatomy of the Attraction Basins: Breaking with the Intuition
   Leticia Hernando, Alexander Mendiburu and Jose A. Lozano
   Evolutionary Computation
   2019 | Journal Paper | Basin of Attraction

Neutrality

1. Neutrality in fitness landscapes
   Christian M. Reidys and Peter F. Stadler
   Applied Mathematics and Computation
   2001 | Journal Paper | Neutrality

2. When Gravity Fails: Local Search Topology
   Jeremy Frank, Peter Cheeseman and John Stutz
   Journal of Artificial Intelligence Research
   1997 | Journal Paper
   Neutrality

3. A quantitative study of neutrality in GP boolean landscapes
   Leonardo Vanneschi, Yuri Pirola and Philippe Collard
   Proc. of the Annual Genetic and Evolutionary Computation Conference (GECCO'06)
   2006 | Conference Paper | Neutrality

Fitness Distribution

1. Re-evaluating genetic algorithm performance under coordinate rotation of benchmark functions. A survey of some theoretical and practical aspects of genetic algorithms
   Ralf Salomon
   Biosystems
   1996 | Journal Paper

2. An Analysis of the Configuration Space of the Maximal Constraint Satisfaction Problem
   Meriema Belaidouni and Jin-Kao Hao
   Proc. of the International Conference on Parallel Problem Solving from Nature (PPSN’VI)
   2000 | Conference Paper

Modality

1. Advanced fitness landscape analysis and the performance of memetic algorithms
   Peter Merz
   Evolutionary Computation
   2004 | Journal Paper

2. How to Detect all Maxima of a Function
   J. Garnier and L. Kallel
   Journal of Theoretical Biology
   2001 | Book Chapter

Ruggedness

1. Towards a General Theory of Adaptive Walks on Rugged Landscapes
   Stuart Kauffman and Simon Levin
   Journal of Theoretical Biology
   1987 | Journal Paper | Adaptive Walks

2. Correlated and Uncorrelated Fitness Landscapes and How to Tell the Difference
   Stuart Kauffman and Simon Levin
   Biological Cybernetics
   1990 | Journal Paper | Autocorrelation

3. Memetic Algorithms for Combinatorial Optimization Problems: Fitness Landscapes and Effective Search Strategies
   Peter Merz
   2000 | PhD Thesis | Autocorrelation

4. Smoothness, Ruggedness and Neutrality of Fitness Landscapes: from Theory to Application
   Vesselin K. Vassilev, Terence C. Fogarty and Julian F. Miller
   Advances in Evolutionary Computing
   1990 | Book Chapter | Autocorrelation, Entropy

5. The Genetic Algorithm and the Structure of the Fitness Landscape
   B. Manderick, M. D. Weger and Piet Spiessens
   Proc. of the International Conference on Genetic Algorithms (ICGA'91)
   1991 | Conference Paper | Correlation Length

6. Towards a Theory of Landscapes
   Peter F. Stadler and Santa Fe Institute
   Complex Systems and Binary Networks
   2007 | Book Chapter | Correlation Length

7. A Measure of Landscapes
   Wim Hordijk
   Evolutionary Computation
   1996 | Journal Paper | Correlation Length

8. Adaptation on rugged landscapes generated by iterated local interactions of neighboring genes
   Mark Lipsitch
   Proc. of the International Conference on Genetic Algorithms (ICGA'91)
   1991 | Conference Paper | Correlation Length

9. Information Characteristics and the Structure of Landscapes
   Vesselin K. Vassilev, Terence C. Fogarty and Julian F. Miller
   Evolutionary Computation
   2000 | Journal Paper | Entropy

10. Quantifying Ruggedness of Continuous Landscapes using Entropy
    Katherine M. Malan and Andries P. Engelbrecht
    Proc. of the 2009 IEEE Congress on Evolutionary Computation (CEC'09)
    2009 | Conference Paper | Entropy

11. Amplitude Spectra of Fitness Landscapes
    Wim Hordijk and Peter F. Stadler
    Advances in Complex Systems
    1998 | Journal Paper | Amplitude Spectra

12. Adaptation on Rugged Landscapes
    Daniel A. Levinthal
    Management Science
    1997 | Journal Paper | Amplitude Spectra

Information Content

1. Landscape Characterization of Numerical Optimization Problems using Biased Scattered Data
   Mario A. Muñoz, Michael Kirley and Saman K. Halgamuge
   Proc. of the 2012 IEEE Congress on Evolutionary Computation (CEC'12)
   2012 | Conference Paper | Information Content

2. Exploratory Landscape Analysis of Continuous Space Optimization Problems Using Information Content
   Mario A. Muñoz, Michael Kirley and Saman K. Halgamuge
   IEEE Transactions on Evolutionary Computation (TEVC)
   2015 | Journal Paper | Information Content

Algorithm Performance and Problem Difficulty

1. Measuring Instance Difficulty for Combinatorial Optimization Problems
   Kate Smith-Miles and Leo Lopes
   Computers & Operations Research
   2012 | Journal Paper | Problem Difficulty

2. The Effects of Constant and Bit-Wise Neutrality on Problem Hardness, Fitness Distance Correlation and Phenotypic Mutation Rates
   Riccardo Poli and Edgar Galvan-Lopez
   IEEE Transactions on Evolutionary Computation (TEVC)
   2012 | Journal Paper

3. Identifying Features of Fitness Landscapes and Relating Them to Problem Difficulty
   I. Moser, M. Gheorghita and A. Aleti
   Evolutionary Computation
   2017 | Journal Paper

4. Algorithm Runtime Prediction: Methods & Evaluation
   Frank Hutter, Lin Xu, Holger H. Hoos and Kevin Leyton-Brown
   Artificial Intelligence
   2014 | Journal Paper | Algorithm Runtime

5. Understanding TSP Difficulty by Learning from Evolved Instances
   Kate Smith-Miles, Jano van Hemert and Xin Yu Lim
   Proc. of the 2010 International Conference on Learning and Intelligent Optimization (LION'10)
   2010 | Conference Paper | Problem Difficulty, Eovoled Instances

6. Evolving Combinatorial Problem Instances That Are Difficult to Solve
   Jano I. van Hemert
   Evolutionary Computation
   2006 | Journal Paper | Problem Difficulty, Eovoled Instances

7. Feature-Based Diversity Optimization for Problem Instance Classification
   Wanru Gao, Samadhi Nallaperuma, Frank Neumann
   Evolutionary Computation
   2021 | Journal Paper | Problem Difficulty

8. Feature-Based Diversity Optimization for Problem Instance Classification
   Wanru Gao, Samadhi Nallaperuma and Frank Neumann
   Evolutionary Computation
   2021 | Journal Paper

9. Understanding the Empirical Hardness of NP-Complete Problems
   Kevin Leyton-Brown, Holger H. Hoos, Frank Hutter and Lin Xu
   Communications of the ACM
   2014 | Journal Paper | Empirical Hardness Model (EHM)

10. Fixed budget computations: a different perspective on run time analysis
    Thomas Jansen and Christine Zarges
    Proc. of the 14th Annual Genetic and Evolutionary Computation Conference (GECCO'12)
    2012 | Conference Paper | Algorithm Performance

11. Performance analysis of randomised search heuristics operating with a fixed budget
    Thomas Jansen and Christine Zarges
    Theoretical Computer Science
    2014 | Journal Paper | Algorithm Performance

12. Towards an analytic framework for analysing the computation time of evolutionary algorithms
    Jun He and Xin Yao
    Artificial Intelligence
    2003 | Journal Paper | Algorithm Performance

13. Empirical hardness models: Methodology and a case study on combinatorial auctions
    Kevin Leyton-Brown, Eugene Nudelman and Yoav Shoham
    Journal of the ACM
    2009 | Journal Paper | Empirical Hardness Model (EHM)

14. A Note on Problem Difficulty Measures in Black-Box Optimization: Classification, Realizations and Predictability
    Jun He, Colin Reeves, Carsten Witt and Xin Yao
    Evolutionary Computation
    2007 | Journal Paper | Problem Difficulty

15. Genetic Algorithm Difficulty and the Modality of Fitness Landscapes
    Jeffrey Horn and David E. Goldberg
    Foundations of Genetic Algorithms
    1995 | Journal Paper

16. A comparison of predictive measures of problem difficulty in evolutionary algorithms
    B. Naudts and L. Kallel
    IEEE Transactions on Evolutionary Computation (TEVC)
    2000 | Journal Paper

Problem-Specific

1. On the Landscapes of Combinatorial Opitmization Problems
   Mohammad-H. Tayarani-N. and Adam Prügel-Bennett
   IEEE Transactions on Evolutionary Computation (TEVC)
   2014 | Journal Paper

Maximum Satisfiability Problem

1. Clustering of Solutions in the Random Satisfiability Problem
   Marc. Mézard, T. Mora, and R. Zecchina
   Physical Review Letter
   2005 | Journal Paper

2. Rigorous location of phase transitions in hard optimization problems
   Dimitris Achlioptas, Assaf Naor and Yuval Peres
   Nature
   2010 | Journal Paper

3. The random K-satisfiability problem: From an analytic solution to an efficient algorithm
   Marc Mézard and Riccardo Zecchina
   Physical Review E
   2002 | Journal Paper

4. Symmetry breaking in population-based optimization
   A. Prugel-Bennett
   IEEE Transactions on Evolutionary Computation (TEVC)
   2004 | Journal Paper

5. Hard and easy distributions of SAT problems
   David Mitchell, Bart Selman and Hector Levesque
   Proc. of the 10th National Conference on Artificial Intelligence (AAAI'92)
   2012 | Conference Paper

6. Experimental results on the crossover point in random 3-SAT
   James M. Crawford and Larry D. Auton
   Artificial Intelligence
   1996 | Journal Paper

7. Determining computational complexity from characteristic ‘phase transitions’
   Rémi Monasson, Riccardo Zecchina, Scott Kirkpatrick, Bart Selman and Lidror Troyansky
   Nature
   1999 | Journal Paper

8. Statistical mechanics methods and phase transitions in optimization problems
   Olivier C. Martin, Rémi Monasson and Riccardo Zecchina
   Theoretical Computer Science
   2001 | Journal Paper

9. Global Landscape Structure and the Random MAX-SAT Phase Transition
   Gabriela Ochoa, Francisco Chicano and Marco Tomassini
   Proc. of the International Conference on Parallel Problem Solving from Nature (PPSN’XVI)
   2020 | Conference Paper

10. Maximum Satisfiability: Anatomy of the Fitness Landscape for a Hard Combinatorial Optimization Problem
    Adam Prugel-Bennett and Mohammad-Hassan Tayarani-Najaran
    IEEE Transactions on Evolutionary Computation (TEVC)
    2012 | Journal Paper

11. Learning the Large-Scale Structure of the MAX-SAT Landscape Using Populations
    Mohamed Qasem; Adam Prügel-Bennett
    IEEE Transactions on Evolutionary Computation (TEVC)
    2010 | Journal Paper

Traveling Salesman Problem

1. An Analysis of the Fitness Landscape of Travelling Salesman Problem
   Mohammad-H. Tayarani-N. and Adam Prügel-Bennett
   Evolutionary Computation
   2016 | Journal Paper

2. A fitness landscape analysis of the travelling thief problem
   Mohamed El Yafrani, Marcella S. R. Martins, Mehdi El Krari, Markus Wagner, Myriam R. B. S. Delgado, Belaïd Ahiod and Ricardo Lüders
   Proc. of the Genetic and Evolutionary Computation Conference (GECCO'18)
   2018 | Conference Paper

3. Runtime Analysis of an Ant Colony Optimization Algorithm for TSP Instances
   Yuren Zhou
   IEEE Transactions on Evolutionary Computation (TEVC)
   2009 | Journal Paper

4. A hybrid heuristic for the traveling salesman problem
   R. Baraglia, J.I. Hidalgo and Perego
   IEEE Transactions on Evolutionary Computation (TEVC)
   2001 | Journal Paper

5. Ant colony system: a cooperative learning approach to the traveling salesman problem
   M. Dorigo and L.M. Gambardella
   IEEE Transactions on Evolutionary Computation (TEVC)
   1997 | Journal Paper

6. An Effective Heuristic Algorithm for the Traveling-Salesman Problem
   S. Lin and B. W. Kernighan
   Operational Research
   1973 | Journal Paper

7. Toward minimal restriction of genetic encoding and crossovers for the two-dimensional Euclidean TSP
   Soonchul Jung and Byung-Ro Moon
   IEEE Transactions on Evolutionary Computation (TEVC)
   2022 | Journal Paper

8. Parameterized Runtime Analyses of Evolutionary Algorithms for the Planar Euclidean Traveling Salesperson Problem
   Andrew M. Sutton, Frank Neumann and Samadhi Nallaperuma
   Evolutionary Computation
   2014 | Journal Paper

9. Feature-Based Diversity Optimization for Problem Instance Classification
   Wanru Gao, Samadhi Nallaperuma, Frank Neumann
   Evolutionary Computation
   2021 | Journal Paper

Number Paritioning Problem

1. Phase Transition and Landscape Properties of the Number Partitioning Problem
   Khulood Alyahya and Jonathan E. Rowe
   Proc. of the European Conference on Evolutionary Computation in Combinatorial Optimization (EvoCOP'14)
   2014 | Conference Paper

2. Heuristics and exact methods for number partitioning
   João Pedro Pedroso and Mikio Kubo
   European Journal of Operational Research
   2010 | Journal Paper

3. Phase Transition in the Number Partitioning Problem
   Stephan Mertens
   Physical Review Letter
   1998 | Journal Paper

4. Phase transition and landscape statistics of the number partitioning problem
   Peter F. Stadler, Wim Hordijk, and José F. Fontanari
   Physical Review E
   2003 | Journal Paper

Knapsack Problem

1. Where are the hard knapsack problems?
   David Pisinger
   Computers & Operations Research
   2005 | Journal Paper

2. Set Theory-Based Operator Design in Evolutionary Algorithms for Solving Knapsack Problems
   Ran Wang and Zichao Zhang
   IEEE Transactions on Evolutionary Computation (TEVC)
   2021 | Journal Paper

3. Multidimensional knapsack problem: a fitness landscape analysis
   Jorge Tavares, Francisco B. Pereira and Ernesto Costa
   IEEE Transactions on Systems, Man, and Cybernetics
   2008 | Journal Paper

NK Landscapes

1. Local Optima Networks of NK Landscapes with Neutrality
   Sébastien Verel, Gabriela Ochoa and Marco Tomassini
   IEEE Transactions on Evolutionary Computation (TEVC)
   2011 | Journal Paper

2. An Analysis of NK Landscapes: Interaction Structure, Statistical Properties, and Expected Number of Local Optima
   Jeffrey Buzas and Jeffrey Dinitz
   IEEE Transactions on Evolutionary Computation (TEVC)
   2014 | Journal Paper

Quadratic Assignment Problem

1. Fitness landscape analysis and memetic algorithms for the quadratic assignment problem
   P. Merz and B. Freisleben
   IEEE Transactions on Evolutionary Computation (TEVC)
   2000 | Journal Paper

2. Quadratic assignment problem: a landscape analysis
   Mohammad-H. Tayarani-N. and Adam Prügel-Bennett
   Evolutionary Intelligence
   2015 | Journal Paper

Landscape Visualization

1. Low-Dimensional Euclidean Embedding for Visualization of Search Spaces in Combinatorial Optimization
   Krzysztof Michalak
   IEEE Transactions on Evolutionary Computation (TEVC)
   2019 | Journal Paper

Paper List of AutoML #

(Still under development)

HPO Essentials

1. Meta-Learning: A Survey
   Joaquin Vanschoren
   arXiv
   2015 | Survey Paper

2. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges
   Bernd Bischl, Martin Binder, Michel Lang, Tobias Pielok, Jakob Richter, Stefan Coors, Janek Thomas, Theresa Ullmann, Marc Becker, Anne-Laure Boulesteix, Difan Deng, Marius Lindauer
   WIREs Data Mining and Knowledge Discovery
   2023 | Survey Paper

3. On hyperparameter optimization of machine learning algorithms: Theory and practice
   Li Yang, Abdallah Shami
   Neurocomputing
   2020 | Survey Paper

4. Hyperparameter optimization in learning systems
   Răzvan Andonie
   Journal of Membrane Computing
   2019 | Survey Paper

5. Beyond Manual Tuning of Hyperparameters
   Frank Hutter, Jörg Lücke, Lars Schmidt-Thieme
   KI - Künstliche Intelligenz
   2018 | Survey Paper

6. A review of automatic selection methods for machine learning algorithms and hyper-parameter values
   Gang Luo
   Network Modeling Analysis in Health Informatics and Bioinformatics
   2016 | Survey Paper | Cited by 313

7. Hyperparameter Optimization
   Matthias Feurer, Frank Hutter
   Automated Machine Learning: Methods, Systems, Challenges
   2019 | Survey Paper

8. Random search for hyper-parameter optimization
   James Bergstra, Yoshua Bengio
   Journal of Machine Learning Research (JMLR)
   2012 | Journal Paper

9. Towards an Empirical Foundation for Assessing Bayesian Optimization of Hyperparameters
   Katharina Eggensperger, Matthias Feurer, Frank Hutter, James Bergstra, Jasper Snoek, Holger Hoos, Kevin Leyton-Brown
   NIPS workshop on Bayesian Optimization in Theory and Practice
   2013 | Conference Paper

10. Practical Bayesian Optimization of Machine Learning Algorithms
    Jasper Snoek, Hugo Larochelle, Ryan P. Adams
    Advances in Neural Information Processing Systems (NIPS'12)
    2012 | Conference Paper

11. Sequential Model-Based Optimization for General Alg. Configuration
    Frank Hutter, Holger H. Hoos, Kevin Leyton-Brown
    LION'11: Proc. of the International Conference on Learning and Intelligent Optimization
    2011 | Conference Paper

12. Algorithms for Hyper-Parameter Optimization
    James Bergstra, Rémi Bardenet, Yoshua Bengio, Balázs Kégl
    Advances in Neural Information Processing Systems (NIPS'11)
    2011 | Conference Paper

13. Practical Recommendations for Gradient-Based Training of Deep Architectures
    Yoshua Bengio
    Neuralnetworks: Tricks of the Trade
    2012 | Book Chapter

14. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures
    James Bergstra, Daniel Yamins, David Cox
    ICML'13: Proc. of the 30th International Conference on Machine Learning
    2013 | Conference Paper

15. Multi-Task Bayesian Optimization
    Kevin Swersky, Jasper Snoek, Ryan P. Adams
    Advances in Neural Information Processing Systems (NIPS'13)
    2013 | Conference Paper

16. Gradient-based Hyperparameter Optimization through Reversible Learning
    Dougal Maclaurin, David Duvenaud, Ryan P. Adams
    ICML'15: Proc. of the 32th International Conference on Machine Learning
    2015 | Conference Paper

17. Efficient Benchmarking of Hyperparameter Optimizers via Surrogates
    Katharina Eggensperger, Frank Hutter, Holger H Hoos, Kevin Leyton-Brown
    AAAI'15: Proceedings of the AAAI Conference on Artificial Intelligence
    2015 | Conference Paper

AutoML

1. AutoML: A survey of the state-of-the-art
   Xin He, Kaiyong Zhao, Xiaowen Chu
   Knowledge-Based Systems
   2012 | Survey Paper Cited by 985

2. Automated Machine Learning: State-of-The-Art and Open Challenges
   Radwa Elshawi, Mohamed Maher, Sherif Sakr
   arXiv
   2019 | Survey Paper Cited by 159

3. Automated Machine Learning: Methods, Systems, Challenges
   Matthias Feurer, Frank Hutter
   Springer
   2019 | Book | Cited by 1,317

4. Taking Human out of Learning Applications: A Survey on Automated Machine Learning
   Quanming Yao, Mengshuo Wang, Yuqiang Chen, Wenyuan Dai, Yu-Feng Li, Wei-Wei Tu, Qiang Yang, Yang Yu
   arXiv
   2019 | Survey Paper | Cited by 356

5. Benchmark and Survey of Automated Machine Learning Frameworks
   Marc-Andre Zoller, Marco F. Huber
   Journal of Artificial Intelligence Research
   2021 | Survey Paper | Cited by 251

Feature Importance

1. An Efficient Approach for Assessing Hyperparameter Importance
   Frank Hutter, Holger Hoos, Kevin Leyton-Brown
   ICML'14: Proc. of the 31th International Conference on Machine Learning
   2014 | Conference Paper

2. Explaining Hyperparameter Optimization via Partial Dependence Plots
   Julia Moosbauer, Julia Herbinger, Giuseppe Casalicchio, Marius Lindauer, Bernd Bischl
   NeurIPS'21: Proc. of the 35th Conference on Neural Information Processing Systems
   2021 | Conference Paper

3. Hyperparameter Importance Across Datasets
   Jan N. van Rijn, Frank Hutter
   KDD ‘18: Proc. of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining
   2018 | Conference Paper

4. Efficient Parameter Importance Analysis via Ablation with Surrogates
   Andre Biedenkapp, Marius Lindauer, Katharina Eggensperger, Frank Hutter
   AAAI'17: Proc. of the Thirty-First AAAI Conference on Artificial Intelligence
   2017 | Conference Paper

Loss Landscape

1. Visualizing the Loss Landscape of Neural Nets
   Hao Li, Zheng Xu, Gavin Taylor, Christoph Studer, Tom Goldstein
   NeurIPS'18: Advances in Neural Information Processing Systems
   2018 | Conference Paper

2. Large Scale Structure of Neural Network Loss Landscapes
   Stanislav Fort, Stanislaw Jastrzebski
   NeurIPS'19: Advances in Neural Information Processing Systems
   2019 | Conference Paper

3. Taxonomizing local versus global structure in neural network loss landscapes
   Yaoqing Yang, Liam Hodgkinson, Ryan Theisen, Joe Zou, Joseph E. Gonzalez, Kannan Ramchandran, Michael W. Mahoney
   NeurIPS'21: Proc. of the 35th Conference on Neural Information Processing Systems
   2021 | Conference Paper

Related Papers

1. Efficient Global Optimization of Expensive Black-Box Functions
   Donald R. Jones, Matthias Schonlau, William J. Welch
   Journal of Global Optimization
   1998 | Journal Paper | Cited by 8,000

2. Effect of the Sampling of a Dataset in the Hyperparameter Optimization Phase over the Efficiency of a Machine Learning Algorithm
   Noemí DeCastro-García, Ángel Luis Muñoz Castañeda, David Escudero García, Miguel V. Carriegos
   Complexity
   2019 | Journal Paper | Cited by 43

Projects and Websites #

• MATILDA
• LON Maps
• Flacco
• COCO

GBFLAT #

• Framwork
• Installation
• Documentation
  • GBFLAT.lon
  • GBFLAT.ils
  • GBFLAT.problems
• Quick Start

Framework #

Under construction.

Installation #

Under construction.

Documentation #

GBFLAT.lon #

class GBFLAT.LON.LocalOptimalNetwork()

This is the general object we use to construct, access, analyze and manipulate LONs.

Methods

LocalOptimalNetwork.read_ils(problem_name, n_runs, n_iters, n, k, seed, path, directed=False, weighted=False, addi_attri=False) -> None

Create LON using recorded data from iterated local search (ILS)

LocalOptimalNetwork.describe() -> pd.DataFrame

Obtain a pandas dataframe containing basic descriptions of the LON.

LocalOptimalNetwork.read_lon(problem_name, n_runs, n_iters, n, k, seed, path, directed=False, weighted=False) -> None

Create LON using saved graph data.

GBFLAT.ils #

GBFLAT.problems #

Quick Start #

Here we provide a simple yet comprehensive guide to illustrate the core functions of GBFLAT. Say, for example, we want to study the landscape characteristics of number partitioning problem (NPP) with 10 items.
We first import core classes and functions from GBFLAT along with some other necessary packages.

• The GBFLAT.Problems module implements various classic combinatorial optimization problems such as NPP, the traveling salesman problem (TSP), and the knapsack problem (KP), etc. Customized problem instances could be easily generated based on these problem classes.
• In GBFLAT.IteratedLocalSearch, we implement ILS method for sampling local optima from the fitness landscape (i.e., search space) of a given problem instance. It also contains various functions for performing neighbourhood exploration, local search as well as perturbation.
• The GBFLAT.LocalOptimalNetwork module contains the essential LON class, which stores a wide range of useful information for performing data mining, manipulation and visualization. In particular, the local optima data is available in both tabular format and graph-structured format, and this is why we always use pandas and networkx library along with GBFLAT.
• Finally, some other depend libraries would sometimes be necessary. For instance, when apply the node embedding method along with dimensionality reduction to draw plain visualizations of LONs, karaterclub and scikit-learn will be needed.

1import pandas as pd
2import networkx as nx
3from karaterclub import HOPE
4from sklean.manifold import TSNE
5from GBFLAT.Problems import NumberPartitioning, Knapsack
6from GBFLAT.LocalOptimalNetwork import LON
7from GBFLAT.IteratedLocalSearch import {
8  ILS, hill_climber, flip_neighbour_explorer, two_bit_flip_pertubator}

After all the necessary modules have been imported, we could now get started by creating an instance of our target problem – an NPP with 10 items. This could be easily done with the following script. Notice that here we also specify k=0.7, which is a control parameter that has impact on the hardness of the NPP. It is also related a phenomenon called “phase transition”. We also set seed=1, which would enable us to come back to this specific instance again at somewhere else.

1# create a problem instance
2instance = NumberPartitioning(n = 10, k = 0.7, seed = 1)

Now we are ready to perform ILS on our created problem instance! We first initialize an ILS searcher object by specifying the total number of independent ILS runs to perform, the maximum number of non-improvement iterations allowed for each run, as well as the method used for neighbour exploration, local search and perturbation.
Here, since the solution vector for NPP is constitued by binary bits, a simple bit-flip-based strategy could be applied to perform neighbour exploration. We adopt hill climbing, a widely used local search strategy to find local optima. After the algorithm encounters a local optimum, a perturbation, which is a two-bits flip here, will be applied to it in the hope to escape.
After properly configured the ils_searcher, we then proceed to conduct the sampling on our target instance. This process here, backended by tqdm, supports parellel processing. Just specify the n_jobs parameter according to the computational budget. In addition, a file path needs to be provided to save the ILS data. The ILS data will be saved as a .csv file, containing a rich amount of information recorded during the sampling.

 1# create an ils_searcher object
 2ils_searcher = ILS(n_runs = 1000, 
 3                   max_iters = 100,
 4                   local_searcher = hill_climbing,
 5                   neighbour_explorer = flip_neighbour_explorer,
 6                   perturbator = two_bit_flip_pertubator)
 7
 8# perform ILS sampling using multiple CPU threads
 9ils_searcher.search(instance = instance, 
10                    path = "ils_data/",
11                    n_jobs = 8)

We now create the LON for our instance. We initialize an LON object and use the LON.read_ils method to construct a LON based on ILS data. We just specifiy the information regard the problem instance and ILS process, these will serve as an unique identifier for the algorithm to locate the ILS file. We then choose whether to consider direction and edge weights in the LON.

 1# create LON object using ILS data
 2lon = LON()
 3lon.read_ils(problem_name = "NPP",
 4             n = 10,
 5             k = 0.7,
 6             seed = 1,
 7             nb_runs = 1000,
 8             nb_iters = 100,
 9             weighted = True,
10             directed = True)

Up to this step, our LON has been constructed! What makes GBFLAT an brilliant tool for graph-based landscape analysis is that the data LON is accessible in both pd.DataFrame and networkx.Graph (or networkx.DiGraph for directed LON) format. This would allow great flexibility and possibility for performing data mining, manipulation and visualization.
Simply access your data via the LON.data or LON.graph property.

1# get LON data
2graph = LON.graph       # get LON data as pandas dataframe object
3data = LON.data         # get LON as NetworkX graph object

The resulting dataframe or graph could power numerious analysis tasks, and here we only present some simpliest examples of these.

1# data manipulation example
2print(data.sort_values(by = "fitness"))
3# graph manipulation example
4sol = [1, 0, 0, 1, 1, 1, 0, 0, 1, 1]
5print(nx.neighbors(graph, sol))

The LON class also has various built-in methods for analyzing LONs. For example, LON.draw_lon method could output a naive visualization of the graph. This is however, only trivial for low-dimensional problems with no more than 1,000 local optima, as when the number of nodes in the graph gets higher, the plot will quickly become messy and not able to depict useful any useful pattern.
Another way for visualizing LON is to leverage node embedding and dimensionality reduction technique. This is implemented by the LON.draw_embedding method. You may obtain a informative LON visualization by changing node embedding and dimensionality reduction method according to the specific task at hand.

1# draw LON as graph
2lon.draw_lon()
3# draw LON in 2D via node embedding and dimensionality reduction
4lon.draw_embedding(model = HOPE(), reducer = TSNE())
5# get statistical description of LON
6lon.describe()

Finally, we could save the constructed LON (along with all the node and edge attributes) to .csv file for quicker accessing next time.

1# save LON
2lon.save_lon(name = "npp_n10_k0.7_seed1")